Duyệt cây theo chiều sâu DFS (Depth First Search)

Để kiểm tra việc duyệt mỗi đỉnh đúng một lần, chúng ta sử dụng một mảng chuaxet[] gồm n phần tử (tương ứng với n đỉnh), nếu đỉnh thứ i đã được duyệt, phần tử tương ứng trong mảng chuaxet[] có giá trị FALSE. Ngược lại, nếu đỉnh chưa được duyệt, phần tử tương ứng trong mảng có giá trị TRUE. Thuật toán có thể được mô tả bằng thủ tục đệ qui DFS () trong đó: chuaxet - là mảng các giá trị logic được thiết lập giá trị TRUE. 
void DFS( int v){ 

 Thăm_Đỉnh(v);

 chuaxet[v]:= FALSE; 

 for ( u ∈ke(v) ) { 

  if (chuaxet[u] ) DFS(u); 

 } 

}
Thủ tục DFS() sẽ thăm tất cả các đỉnh cùng thành phần liên thông với mỗi đỉnh đúng một lần. Để đảm bảo duyệt tất cả các đỉnh của đồ thị (có thể có nhiều thành phần liên thông), chúng ta chỉ cần thực hiện duyệt như sau: 
for (i=1; i≤n ; i++)

 chuaxet[i]:= TRUE; /* thiết lập giá trị ban đầu cho mảng chuaxet[]*/

for (i=1; i≤n ; i++)

 if (chuaxet[i] )

  DFS( i);

Đồ thị - Tìm kiếm theo chiều sâu DFS

Đồ thị - Tìm kiếm theo chiều sâu DFS

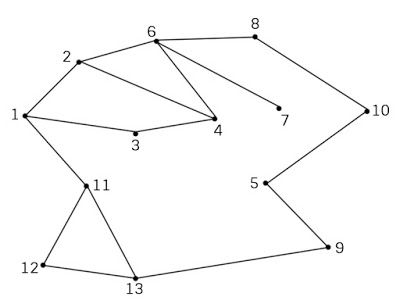
Kết quả duyệt: 1, 2, 4, 3, 6, 7, 8, 10, 5, 9, 13, 11, 12
STT
Đỉnh bắt đầu duyệt
Các đỉnh đã duyệt
Các đỉnh chưa duyệt
1 DFS(1) 1 2,3,4,5,6,7,8,9,10,11,12,13
2 DFS(2) 1,2 3,4,5,6,7,8,9,10,11,12,13
3 DFS(4) 1,2,4 3,5,6,7,8,9,10,11,12,13
4 DFS(3) 1,2,4,3 5,6,7,8,9,10,11,12,13
5 DFS(6) 1,2,4,3,6 5,7,8,9,10,11,12,13
6 DFS(7) 1,2,4,3,6,7 5,8,9,10,11,12,13
7 DFS(8) 1,2,4,3,6,7,8 5,9,10,11,12,13
8 DFS(10) 1,2,4,3,6,7,8,10 5,9,11,12,13
9 DFS(10) 1,2,4,3,6,7,8,10,5 9,11,12,13
10 DFS(9) 1,2,4,3,6,7,8,10,5,9 11,12,13
11 DFS(13) 1,2,4,3,6,7,8,10,5,9,13 11,12
12 DFS(11) 1,2,4,3,6,7,8,10,5,9,13,11 12
13 DFS(12) 1,2,4,3,6,7,8,10,5,9,13,11,12 Ѳ

DFS.IN

13
0    1    1    0    0    0    0    0    0    0    1    0    0
1    0    0    1    0    1    0    0    0    0    0    0    0
1    0    0    1    0    0    0    0    0    0    0    0    0
0    1    1    0    0    1    0    0    0    0    0    0    0
0    0    0    0    0    0    0    0    1    1    0    0    0
0    1    0    1    0    0    1    1    0    0    0    0    0
0    0    0    0    0    1    0    0    0    0    0    0    0
0    0    0    0    0    1    0    0    0    1    0    0    0
0    0    0    0    1    0    0    0    0    0    0    0    1
0    0    0    0    1    0    0    1    0    0    0    0    0
1    0    0    0    0    0    0    0    0    0    0    1    1
0    0    0    0    0    0    0    0    0    0    1    0    1
0    0    0    0    0    0    0    0    1    0    1    1    0

Chương trình cài đặt bằng C/C++

#include<iostream>

#include<conio.h>

using namespace std;

#define MAX  100 

#define TRUE 1 

#define FALSE 0 

int G[MAX][MAX], n, chuaxet[MAX]; 

void Init(){ 

 freopen("DFS.IN", "r", stdin); 

 cin>>n; 

 cout<<"So dinh cua ma tran n = "<<n<<endl;

 //nhap ma tran lien ke.

 for(int i=1; i<=n;i++){ 

  for(int j=1; j<=n;j++){ 

   cin>>G[i][j]; 

  } 

 } 

} 

/* Depth First Search */

void DFS(int G[][MAX], int n, int v, int chuaxet[]){ 

 cout<<"Duyet dinh : "<<v<<endl;

 int u; 

 chuaxet[v]=FALSE; 

 for(u=1; u<=n; u++){ 

  if(G[v][u]==1 && chuaxet[u]) 

   DFS(G,n, u, chuaxet); 

 } 

} 

void main(void){ 

 Init(); 

 for(int i=1; i<=n; i++) 

  chuaxet[i]=TRUE; 

 for(int i=1; i<=n;i++) 

  if(chuaxet[i]) 

   DFS( G,n, i, chuaxet); 

 _getch(); 

}

Tham khảo

Source code tham khảo