Mô tả

  • Giống như Prim, thuật toán Kruskal cũng tìm cây khung nhỏ nhất nhưng không phụ thuộc vào điểm bắt đầu.
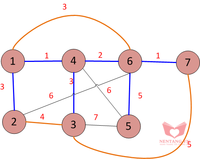
  • Hình 1, đồ thị như sau:

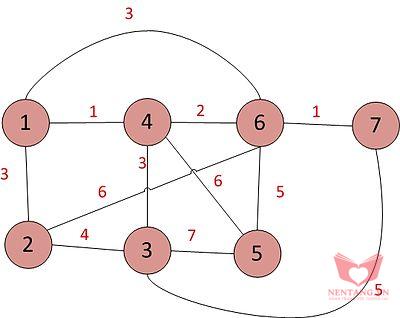
Bước 1: lập bảng, liệt kê tăng dần theo trọng số của các cạnh.

Đỉnh U Đỉnh V Trọng số
1 4 1
6 7 1
4 6 2
1 2 3
1 6 3
3 4 3
2 3 4
3 7 5
5 6 5
2 6 6
4 5 6
3 5 7

Bước 2: dựa vào thứ tự bảng trên để đánh giá cạnh đó có thuộc cây khung tối tiểu hay không. Một cạnh thõa điều kiện khi nó không góp phần tạo thành một chu trình với tất cả các cạnh đã tìm được.

1-4-1: Ta nhận thấy cạnh 1-4 không tạo ra một chu trình nào. Vì vậy, thêm 1-4 vào tập hợp 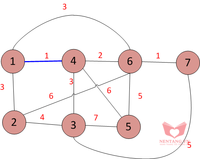6-7-1: Ta nhận thấy cạnh 6-7 không tạo ra một chu trình nào. Vì vậy, thêm 6-7 vào tập hợp 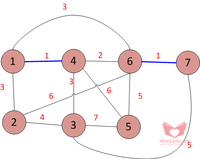4-6-2: Ta nhận thấy cạnh 4-6 không tạo ra một chu trình nào. Vì vậy, thêm 4-6 vào tập hợp 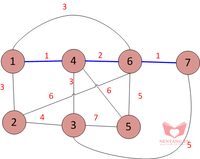 1-2-3: Ta nhận thấy cạnh 1-2 không tạo ra một chu trình nào. Vì vậy, thêm 1-2 vào tập hợp 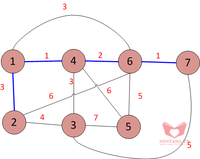1-6-3: Ta nhận thấy cạnh 1-6 tạo ra một chu trình. Không thêm vào tập hợp. 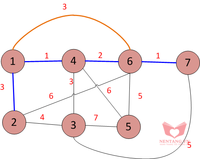2-3-4: Ta nhận thấy cạnh 2-3 tạo ra một chu trình. Không thêm vào tập hợp. 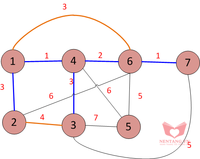3-7-5: Ta nhận thấy cạnh 3-7 tạo ra một chu trình. Không thêm vào tập hợp. 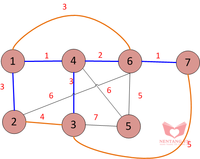5-6-5: Ta nhận thấy cạnh 5-6 không tạo ra một chu trình nào. 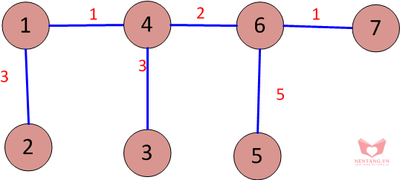Vì vậy, thêm 5-6 vào tập hợp CÂY BAO TRÙM THU ĐƯỢC, Hình 10:

Cài đặt

– Bước 1, khai báo các biến, ta sẽ không sử dụng ma trận kề để lưu đồ thị, mà sẽ sử dụng danh sách các cạnh đã khai báo để lưu từng cạnh, vì vậy khi nhập dữ liệu vào, ta cần gán dữ liệu vào danh sách các cạnh: Các hàm cần thiết:
  • Hàm find(v):  tìm nút gốc của đỉnh v.
  • Hàm Union(u, v): hàm nối 2 đỉnh lại với nhau.
  • Hàm sort(): dùng để sắp xếp các cạnh tăng dần theo trọng số
  Tham khảo https://lhchuong.wordpress.com/2014/10/03/thuat-toan-kruskal-tim-cay-bao-trum-nho-nhat/