Bài toán: Cho đồ thị G=(V, E). Trong đó V là tập đỉnh, E là tập cạnh của đồ thị. Hãy tìm đường đi từ đỉnh s ∈ Vtới đỉnh t ∈ V.
Thủ tục BFS(s) hoặc DFS(s) cho phép ta duyệt các đỉnh cùng một thành phần liên thông với s. Như vậy, nếu trong số các đỉnh liên thông với s chứa t thì chắc chắn có đường đi từ s đến t. Nếu trong số các đỉnh liên thông với s không chứa t thì không tồn tại đường đi từ s đến t. Do vậy, chúng ta chỉ cần gọi tới thủ tục DFS(s) hoặc BFS(s) và kiểm tra xem đỉnh t có thuộc thành phần liên thông với s hay không. Điều này được thực hiện đơn giản thông qua mảng trạng thái chuaxet[]. Nếu chuaxet[t] =False thì có nghĩa t cùng thành phần liên thông với s. Ngược lại chuaxet[t] = True thì t không cùng thành phần liên thông với s.
Để ghi nhận đường đi từ s đến t, ta sử dụng một mảng truoc[] thiết lập giá trị ban đầu là 0.Trong quá trình duyệt, ta thay thế giá trị của truoc[v] để ghi nhận đỉnh đi trước đỉnh v trong đường đi tìm kiếm từ s đến v. Khi đó, trong thủ tục DFS(v) ta chỉ cần thay đổi lại như sau:
void DFS( int v){
chuaxet[v]:= FALSE;
for ( u ∈ke(v) ) {
if (chuaxet[u] ) {
truoc[u]=v;
DFS(u);
}
}
}
Đối với thủ tục BFS(v) được thay đổi lại như sau:
void BFS(int u){
queue = φ;
u <= queue; /*nạp u vào hàng đợi*/
chuaxet[u] = false;/* đổi trạng thái của u*/
while (queue ≠ φ) { /* duyệt tới khi nào hàng đợi rỗng*/
queue<=p; /*lấy p ra từkhỏi hàng đợi*/
for (v ∈ke(p) ) {/* đưa các đỉnh v kềvới p nhưng chưa được xét vào hàng đợi*/
if (chuaxet[v] ) {
v<= queue; /*đưa v vào hàng đợi*/
chuaxet[v] = false;/* đổi trạng thái của v*/
truoc[v]=p;
}
}
} /* end while*/
}/* end BFS*/
Kết quả đường đi được đọc ngược lại thông qua thủ tục Result() như sau:
void Result(void){
if(truoc[t]==0){
<Không có đường đi từs đến t>;
return;
}
j = t;
while(truoc[j]!=s){
<thăm đỉnh j>;
j=truoc[j];
}
<thăm đỉnh s>;
}
Ví dụ. Tìm đường đi từ đỉnh 1 đến đỉnh 7 bằng thuật toán tìm kiếm theo chiều rộng với đồ thị dưới đây:
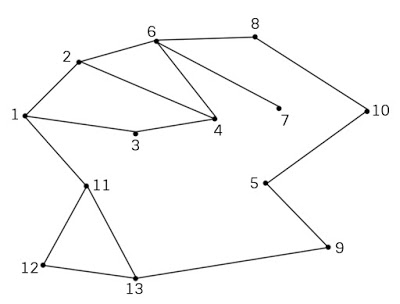
Tìm đường đi giữa đỉnh 1 đến đỉnh 7 của đồ thị
Ta có, BFS(1) = 1,2,3,11,4,6,12,13,7,8,9,10,5. Rõ ràng chuaxet[7] = True nên có đường đi từ đỉnh 1 đến đỉnh 7. Bây giờ ta xác định giá trị trong mảng truoc[] để có kết quả đường đi đọc theo chiều ngược lại. Truoc[7] = 6; truoc[6] = 2; truoc[2] =1=> đường đi từ đỉnh 1 đến đỉnh 7 là 1 =>2=>6=>7.
Chương trình cài đặt
#include<iostream>
#include<conio.h>
using namespace std;
#define MAX 100
#define TRUE 1
#define FALSE 0
int n;//số đỉnh của đồ thị.
int truoc[MAX], chuaxet[MAX], queue[MAX];//mảng đánh dấu.
int A[MAX][MAX];// ma trận kề của đồ thị.
int s;//đỉnh đầu.
int t;//đỉnh cuối.
void Init(void){
freopen("lienth.IN", "r",stdin);
cin>>n;
cout<<"So dinh do thi: "<<n<<endl;
cin>>s>>t;
cout<<"Dinh dau:"<<s<<endl;
cout<<"Dinh cuoi:"<<t<<endl;
for(int i=1; i<=n;i++){
for(int j=1; j<=n;j++){
cin>>A[i][j];
}
}
for(int i=1; i<=n;i++){
chuaxet[i]=TRUE;
truoc[i]=0;
}
fclose(stdin);
}
void Result(void){
if(truoc[t]==0){
cout<<"Khong co duong di tu "<<s<< " den "<<t;
return;
}
cout<<"Duong di tu "<<s<<" den "<<t<<" la: ";
int j = t;
cout<<t<<"<=";
while(truoc[j]!=s){
cout<<truoc[j]<<"<=";
j=truoc[j];
}
cout<<s;
}
/* Breadth First Search */
void BFS(int s) {
int dauQ, cuoiQ, u;
dauQ=1;cuoiQ=1;//khởi tạo queue.
queue[dauQ]=s;chuaxet[s]=FALSE; //thêm đỉnh đầu vào queue.
while (dauQ<=cuoiQ){//queue chưa rỗng.
u=queue[dauQ];//lấy đỉnh u trong queue.
dauQ=dauQ+1;
for (int p=1; p<=n;p++){
if(A[u][p] && chuaxet[p]){
cuoiQ=cuoiQ+1;
queue[cuoiQ]=p;
chuaxet[p]=FALSE;
truoc[p]=u;
}
}
}
}
void main(void){
Init();
BFS(s);
Result();
getch();
}
Ma trận liền kề lienth.IN
13
1 7
0 1 1 0 0 0 0 0 0 0 1 0 0
1 0 0 1 0 1 0 0 0 0 0 0 0
1 0 0 1 0 0 0 0 0 0 0 0 0
0 1 1 0 0 1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 1 1 0 0 0
0 1 0 1 0 0 1 1 0 0 0 0 0
0 0 0 0 0 1 0 0 0 0 0 0 0
0 0 0 0 0 1 0 0 0 1 0 0 0
0 0 0 0 1 0 0 0 0 0 0 0 1
0 0 0 0 1 0 0 1 0 0 0 0 0
1 0 0 0 0 0 0 0 0 0 0 1 1
0 0 0 0 0 0 0 0 0 0 1 0 1
0 0 0 0 0 0 0 0 1 0 1 1 0
Output của chương trình.
So dinh cua do thi: 13
Dinh dau: 1
Dinh Cuoi: 7
Duong di tu 1 den 7 la: 7<=6<=2<=1
|
