


Chương 2-Bài 12. Duyệt cây theo chiều rộng BFS (Breadth First Search)
Tác giả: Dương Nguyễn Phú Cường
Số phút học: 47 phút
Số phút học: 47 phút
Ngày đăng:
4/3/2026, 15:9
Lượt xem: 2067
Khác với thuật toán tìm kiếm theo chiều sâu, thuật toán tìm kiếm theo chiều rộng thay thế việc sử dụng stack bằng hàng đợi queue. Trong thủ tục này, đỉnh được nạp vào hàng đợi đầu tiên là v, các đỉnh kề với v ( v1, v2,..., vk) được nạp vào queue kế tiếp. Quá trình duyệt tiếp theo được bắt đầu từ các đỉnh còn có mặt trong hàng đợi.
Để ghi nhận trạng thái duyệt các đỉnh của đồ thị, ta cũng vẫn sử dụng mảng chuaxet[] gồm n phần tử thiết lập giá trị ban đầu là TRUE. Nếu đỉnh i của đồ thị đã được duyệt, giá trị chuaxet[i] sẽ nhận giá trị FALSE. Thuật toán dừng khi hàng đợi rỗng.
Thủ tục BFS dưới đây thể hiện quá trình thực hiện của thuật toán:
void BFS(int u){
queue = φ;
u <= queue; /*nạp u vào hàng đợi*/
chuaxet[u] = false;/* đổi trạng thái của u*/
while (queue ≠ φ) { /* duyệt tới khi nào hàng đợi rỗng*/
queue<=p; /*lấy p ra từ khỏi hàng đợi*/
Thăm_Đỉnh(p); /* duyệt xong đỉnh p*/
for (v ∈ke(p) ) {/* đưa các đỉnh v kề với p nhưng chưa được xét vào hàng đợi*/
if (chuaxet[v] ) {
v<= queue; /*đưa v vào hàng đợi*/
chuaxet[v] = false;/* đổi trạng thái của v*/
}
}
} /* end while*/
}/* end BFS*/
Thủ tục BFS sẽ thăm tất cả các đỉnh cùng thành phần liên thông với u. Để thăm tất cả các đỉnh của đồ thị, chúng ta chỉ cần thực hiện đoạn chương trình dưới đây:
for (u=1; u≤n; u++) chuaxet[u] = TRUE; for (u∈V ) if (chuaxet[u] ) BFS(u);
Đồ thị - Tìm kiếm theo chiều rộng BFS
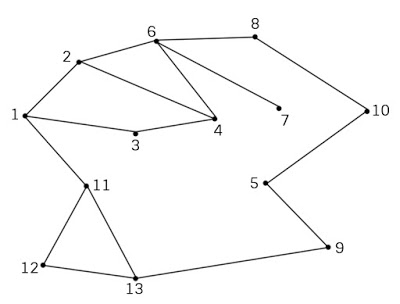
BFS.IN
13 0 1 1 0 0 0 0 0 0 0 1 0 0 1 0 0 1 0 1 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 1 0 1 0 0 1 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 1 0 1 1 0
Chạy tay
|
STT |
Các đỉnh đã duyệt |
Các đỉnh trong hàng đợi |
Các đỉnh còn lại |
| 1 | Ѳ | Ѳ | 1,2,3,4,5,6,7,8,9,10,11,12,13 |
| 2 | 1 | 2,3,11 | 4,5,6,7,8,9,10,12,13 |
| 3 | 1,2 | 3,11,4,6 | 5,7,8,9,10,12,13 |
| 4 | 1,2,3 | 11,4,6 | 5,7,8,9,10,12,13 |
| 5 | 1,2,3,11 | 4,6,12,13 | 5,7,8,9,10 |
| 6 | 1,2,3,11,4 | 6,12,13 | 5,7,8,9,10 |
| 7 | 1,2,3,11,4,6 | 12,13,7,8 | 5,9,10 |
| 8 | 1,2,3,11,4,6,12 | 13,7,8 | 5,9,10 |
| 9 | 1,2,3,11,4,6,12,13 | 7,8,9 | 5,10 |
| 10 | 1,2,3,11,4,6,12,13,7 | 8,9 | 5,10 |
| 11 | 1,2,3,11,4,6,12,13,7,8 | 9,10 | 5 |
| 12 | 1,2,3,11,4,6,12,13,7,8,9 | 10,5 | Ѳ |
| 13 | 1,2,3,11,4,6,12,13,7,8,9,10 | 5 | Ѳ |
| 14 | 1,2,3,11,4,6,12,13,7,8,9,10,5 | Ѳ | Ѳ |
Chương trình cài đặt bằng C/C++
#include<iostream>
#include<conio.h>
using namespace std;
#define MAX 100
#define TRUE 1
#define FALSE 0
int G[MAX][MAX], n, chuaxet[MAX], QUEUE[MAX];
void Init(){
freopen("BFS.IN","r",stdin);
cin>>n;
cout<<"So dinh cua do thi n = "<<n<<endl;
//nhap ma tran lien ke.
for(int i=1; i<=n;i++){
for(int j=1; j<=n;j++){
cin>>G[i][j];
}
}
for(int i=1; i<=n;i++){
chuaxet[i]=TRUE;
}
}
/* Breadth First Search */
void BFS(int i){
int u,dauQ, cuoiQ;
dauQ=1; cuoiQ=1;QUEUE[cuoiQ]=i;chuaxet[i]=FALSE;
/* thiết lập hàng đợi với đỉnh đầu là i*/
while(dauQ<=cuoiQ){
u=QUEUE[dauQ];// lấy đỉnh u ra khỏi queue.
cout<<"duyet dinh: "<<u<<endl;
dauQ=dauQ+1; /* duyệt đỉnh đầu hàng đợi*/
for(int j=1; j<=n;j++){
if(G[u][j]==1 && chuaxet[j] ){
cuoiQ=cuoiQ+1;
QUEUE[cuoiQ]=j;
chuaxet[j]=FALSE;
}
}
}
}
void main(void){
Init();
for(int i=1; i<=n; i++)
if (chuaxet[i])
BFS(i);
_getch();
}
Bình luận
Bình luận của bạnNền tảng các kiến thức học tập
Cùng nhau học tập, khám phá các kiến thức nền tảng về Lập trình web, mobile, database nhé.
Nền tảng kiến thức - Hành trang tới tương lai hân hạnh phục vụ Quý khách!
Khám phá, trải nghiệm ngay

Vui lòng đăng nhập để gởi bình luận!
Đăng nhậpChưa có bình luận nào!