Chương trình học
Bài toán: Cho đồ thị G=(V, E). Trong đó V là tập đỉnh, E là tập cạnh của đồ thị. Hãy tìm đường đi từ đỉnh s ∈ Vtới đỉnh t ∈ V.
Thủ tục BFS(s) hoặc DFS(s) cho phép ta duyệt các đỉnh cùng một thành phần liên thông với s. Như vậy, nếu trong số các đỉnh liên thông với s chứa t thì chắc chắn có đường đi từ s đến t. Nếu trong số các đỉnh liên thông với s không chứa t thì không tồn tại đường đi từ s đến t. Do vậy, chúng ta chỉ cần gọi tới thủ tục DFS(s) hoặc BFS(s) và kiểm tra xem đỉnh t có thuộc thành phần liên thông với s hay không. Điều này được thực hiện đơn giản thông qua mảng trạng thái chuaxet[]. Nếu chuaxet[t] =False thì có nghĩa t cùng thành phần liên thông với s. Ngược lại chuaxet[t] = True thì t không cùng thành phần liên thông với s.
Để ghi nhận đường đi từ s đến t, ta sử dụng một mảng truoc[] thiết lập giá trị ban đầu là 0.Trong quá trình duyệt, ta thay thế giá trị của truoc[v] để ghi nhận đỉnh đi trước đỉnh v trong đường đi tìm kiếm từ s đến v. Khi đó, trong thủ tục DFS(v) ta chỉ cần thay đổi lại như sau:
Ta có, BFS(1) = 1,2,3,11,4,6,12,13,7,8,9,10,5. Rõ ràng chuaxet[7] = True nên có đường đi từ đỉnh 1 đến đỉnh 7. Bây giờ ta xác định giá trị trong mảng truoc[] để có kết quả đường đi đọc theo chiều ngược lại. Truoc[7] = 6; truoc[6] = 2; truoc[2] =1=> đường đi từ đỉnh 1 đến đỉnh 7 là 1 =>2=>6=>7.
void DFS( int v){
chuaxet[v]:= FALSE;
for ( u ∈ke(v) ) {
if (chuaxet[u] ) {
truoc[u]=v;
DFS(u);
}
}
}
Đối với thủ tục BFS(v) được thay đổi lại như sau:
void BFS(int u){
queue = φ;
u <= queue; /*nạp u vào hàng đợi*/
chuaxet[u] = false;/* đổi trạng thái của u*/
while (queue ≠ φ) { /* duyệt tới khi nào hàng đợi rỗng*/
queue<=p; /*lấy p ra từkhỏi hàng đợi*/
for (v ∈ke(p) ) {/* đưa các đỉnh v kềvới p nhưng chưa được xét vào hàng đợi*/
if (chuaxet[v] ) {
v<= queue; /*đưa v vào hàng đợi*/
chuaxet[v] = false;/* đổi trạng thái của v*/
truoc[v]=p;
}
}
} /* end while*/
}/* end BFS*/
Kết quả đường đi được đọc ngược lại thông qua thủ tục Result() như sau:
void Result(void){
if(truoc[t]==0){
<Không có đường đi từs đến t>;
return;
}
j = t;
while(truoc[j]!=s){
<thăm đỉnh j>;
j=truoc[j];
}
<thăm đỉnh s>;
}
Ví dụ. Tìm đường đi từ đỉnh 1 đến đỉnh 7 bằng thuật toán tìm kiếm theo chiều rộng với đồ thị dưới đây:
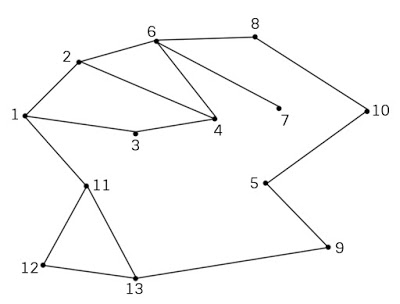
Tìm đường đi giữa đỉnh 1 đến đỉnh 7 của đồ thị
Chương trình cài đặt
#include<iostream>
#include<conio.h>
using namespace std;
#define MAX 100
#define TRUE 1
#define FALSE 0
int n;//số đỉnh của đồ thị.
int truoc[MAX], chuaxet[MAX], queue[MAX];//mảng đánh dấu.
int A[MAX][MAX];// ma trận kề của đồ thị.
int s;//đỉnh đầu.
int t;//đỉnh cuối.
void Init(void){
freopen("lienth.IN", "r",stdin);
cin>>n;
cout<<"So dinh do thi: "<<n<<endl;
cin>>s>>t;
cout<<"Dinh dau:"<<s<<endl;
cout<<"Dinh cuoi:"<<t<<endl;
for(int i=1; i<=n;i++){
for(int j=1; j<=n;j++){
cin>>A[i][j];
}
}
for(int i=1; i<=n;i++){
chuaxet[i]=TRUE;
truoc[i]=0;
}
fclose(stdin);
}
void Result(void){
if(truoc[t]==0){
cout<<"Khong co duong di tu "<<s<< " den "<<t;
return;
}
cout<<"Duong di tu "<<s<<" den "<<t<<" la: ";
int j = t;
cout<<t<<"<=";
while(truoc[j]!=s){
cout<<truoc[j]<<"<=";
j=truoc[j];
}
cout<<s;
}
/* Breadth First Search */
void BFS(int s) {
int dauQ, cuoiQ, u;
dauQ=1;cuoiQ=1;//khởi tạo queue.
queue[dauQ]=s;chuaxet[s]=FALSE; //thêm đỉnh đầu vào queue.
while (dauQ<=cuoiQ){//queue chưa rỗng.
u=queue[dauQ];//lấy đỉnh u trong queue.
dauQ=dauQ+1;
for (int p=1; p<=n;p++){
if(A[u][p] && chuaxet[p]){
cuoiQ=cuoiQ+1;
queue[cuoiQ]=p;
chuaxet[p]=FALSE;
truoc[p]=u;
}
}
}
}
void main(void){
Init();
BFS(s);
Result();
getch();
}
Ma trận liền kề lienth.IN
13 1 7 0 1 1 0 0 0 0 0 0 0 1 0 0 1 0 0 1 0 1 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 1 0 1 0 0 1 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 1 0 1 1 0Output của chương trình. So dinh cua do thi: 13 Dinh dau: 1 Dinh Cuoi: 7 Duong di tu 1 den 7 la: 7<=6<=2<=1
Các bài học
Bài học trước Bài học tiếp theo
Chương trình học
Bao gồm Module, Chương, Bài học, Bài tập, Kiểm tra...Chương trình học
Bài học trước Bài học tiếp theo