


Chương 2-Bài 30. Lab 8 - Tìm luồng cực đại - sử dụng thuật toán Ford - Fulkerson
Tác giả: Dương Nguyễn Phú Cường
Số phút học: 46 phút
Số phút học: 46 phút
Ngày đăng:
12/3/2026, 9:19
Lượt xem: 1599
Đề bài
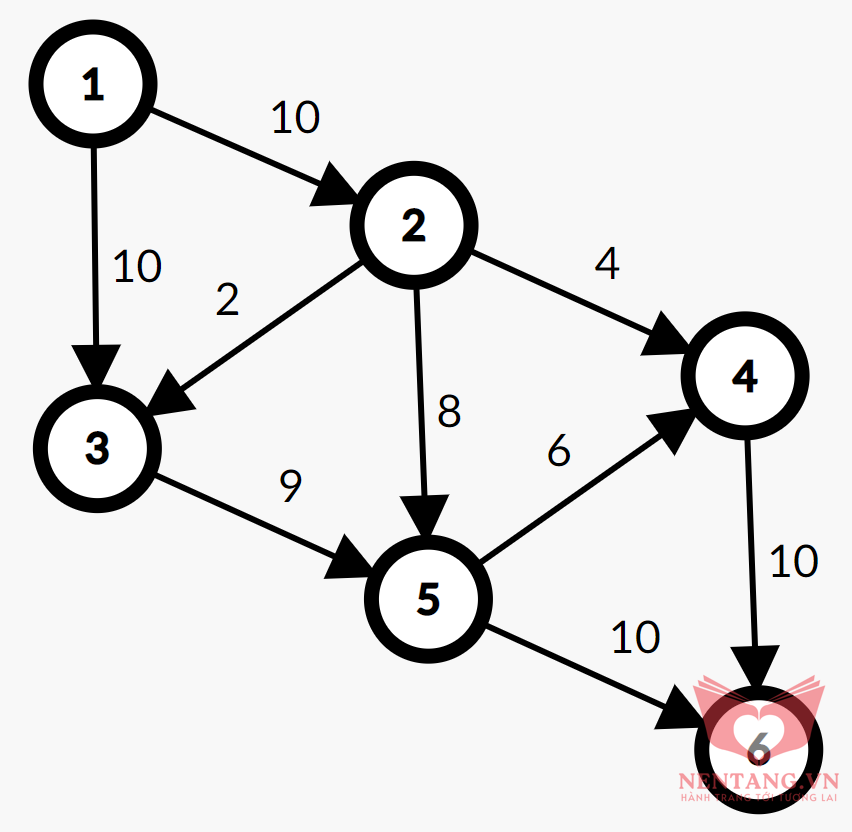
Cho mạng G có n đỉnh và m cạnh, đỉnh phát là 0, và đỉnh thu là n-1. Hãy tìm luồng f* trong mạng sao cho giá trị val(f*) của luồng f* là lớn nhất.Input
- Dòng đầu tiên chứa 2 số n, m là số đỉnh và số cung trong mạng G.
- M dòng tiếp theo, mỗi dòng là 3 số u, v, c cho biết cung nối từ u đến v có trọng số là c.
Output
- Ghi một số nguyên dương cho biết giá trị luồng cực đại tìm được.
| Input | Output |
| 6 9 1 2 10 1 3 10 2 3 2 2 4 4 2 5 8 3 5 9 4 6 10 5 4 6 5 6 10 | 19 |
Minh họa
Giải
- Source code:
#include<bits/stdc++.h>
#include<iostream>
using namespace std;
using ll = long long;
const int maxN = 1001;
const int INF = 1e9; // so vo cung
const int NULL_INT = -1;
int n, m; // n: so dinh, m: so canh
int s, t; // s: dinh bat dau, t: dinh ket thuc
vector<pair<int, int>> adj[maxN];
int parent[maxN];
int RC[maxN][maxN]; // luu tru cung xuoi, cung nguoc
int add_flow; // luu tru gia tri luong cuc dai
void inp() {
cin >> n >> m;
for(int i = 0; i < m; i++) {
int x, y, z;
cin >> x >> y >> z;
adj[x].push_back({y, z});
// Do thi co huong thi comment dong code sau
adj[y].push_back({x, z});
// Luu tru gia tri trong so
RC[x][y] = z;
}
}
void dfs(int u) {
//cout << u << " ";
for(auto item: adj[u]) {
int v = item.first;
int w = item.second;
// Neu dinh v chua duoc tham
if(parent[v] == -1 && RC[u][v]) {
parent[v] = u; // Ghi nhan cha cua v la u
add_flow = min(add_flow, RC[u][v]);
dfs(v);
}
}
}
// Giai thuat Ford_Fulkerson
// s: dinh bat dau
// t: dinh ket thuc
// n: so luong dinh
int maxFlow_Ford_Fulkerson(int s, int t, int n) {
int flow = 0;
while(1) {
// Khoi tao
memset(parent, NULL_INT, sizeof(parent));
parent[s] = 0;
add_flow = INT_MAX;
dfs(s);
if(parent[t] == NULL_INT) {
break;
}
flow += add_flow;
int v = t;
while(v != s) {
int u = parent[v];
RC[v][u] += add_flow; // cung nguoc
RC[u][v] -= add_flow; // cung xuoi
v = u;
}
}
return flow;
}
int main() {
// Chuyen NHAP, XUAT thanh file
freopen("lab_8_input.INP", "r", stdin);
freopen("lab_8_output.OUT", "w", stdout);
// INPUT
inp();
// OUTPUT
int s = 1;
int t = n;
cout << maxFlow_Ford_Fulkerson(s, t, n);
return 0;
}
Bình luận
Bình luận của bạnNền tảng các kiến thức học tập
Cùng nhau học tập, khám phá các kiến thức nền tảng về Lập trình web, mobile, database nhé.
Nền tảng kiến thức - Hành trang tới tương lai hân hạnh phục vụ Quý khách!
Khám phá, trải nghiệm ngay

Vui lòng đăng nhập để gởi bình luận!
Đăng nhậpChưa có bình luận nào!